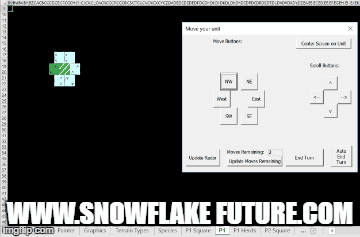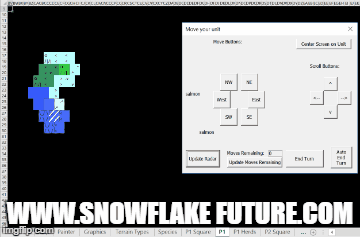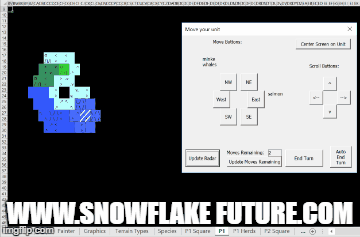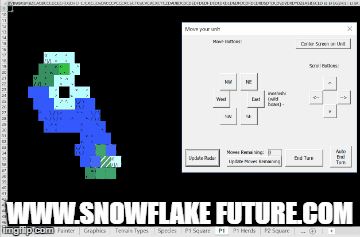
This new game from Coast of Kobe makes good use of the "Exodus to Kobe" map generation algorithms.
Read more about it here: https://coastofkobe.wordpress.com/about/
Snowflake Future
Tuesday, August 1, 2017
Wednesday, May 10, 2017
Kansai Rail Simulator - Download Link
Kansai Rail Simulator is now available for download: https://sourceforge.net/projects/kansai-rail-simulator/files/
Please post questions to the Disqus forum below.
Please post questions to the Disqus forum below.
Saturday, March 25, 2017
Kansai Rail Simulator - LP - Russia
Let's Play (Russia)
In this game, I started by building a single surface rail line along the coast, and I chose a "sparse" strategy, building track-only (no stations) on less populated tiles. By turn 58, this line was net profitable:
Next, I moved to the south, where cities were beginning to grow on the forest's edge. By turn 65, I had a small surface rail line there (4 stations):
By turn 70, most of the population was concentrated in 11 major cities (black border in screenshot below). For the two big cities on the west coast, I chose the names Vancouver and Seattle:
At this time (turn 70), Seattle was a more desirable location than Vancouver:
That's because only Seattle was connected to my new subway system in the south:
The "Arctic Line" and "Moscow Metro Line" are highlighted below (Arctic Line in grey, Moscow Metro in red):
I planned to extend the Moscow Metro along the coast to connect with the big cities in the north, but at that time (turn 70), acquiring land in Vancouver was expensive, due to a shortage of available available land, due in turn to Vancouver's relatively high population (1.338 million):
I decided to wait a couple turns before extending the Moscow Metro northwards into Seattle. This gave people time to migrate to the more desirable location (from Vancouver to Seattle). By turn 72, drawn by Seattle's superior connectivity in the rail network, over 300,000 people had migrated from Vancouver. This made land acquisition in Vancouver much cheaper.
By turn 73, I had four cities over population one million (black border):
On turns 79-81 I used the trade winds to rapidly explore the sea in the far south and south-east.
By turn 102, I had 9 big million-plus cities:
Land value in these cities was bolstered by two metro lines. A second line was required in the north-western forest due to geometric constraints (branching is not allowed):
On turn 168, I stopped building, and just started saving money to get the 6th and final tech.
Game finished on turn 173. At this time, I had 6 cities over 2.5 million:
In this game, I started by building a single surface rail line along the coast, and I chose a "sparse" strategy, building track-only (no stations) on less populated tiles. By turn 58, this line was net profitable:
Next, I moved to the south, where cities were beginning to grow on the forest's edge. By turn 65, I had a small surface rail line there (4 stations):
By turn 70, most of the population was concentrated in 11 major cities (black border in screenshot below). For the two big cities on the west coast, I chose the names Vancouver and Seattle:
At this time (turn 70), Seattle was a more desirable location than Vancouver:
That's because only Seattle was connected to my new subway system in the south:
The "Arctic Line" and "Moscow Metro Line" are highlighted below (Arctic Line in grey, Moscow Metro in red):
I planned to extend the Moscow Metro along the coast to connect with the big cities in the north, but at that time (turn 70), acquiring land in Vancouver was expensive, due to a shortage of available available land, due in turn to Vancouver's relatively high population (1.338 million):
I decided to wait a couple turns before extending the Moscow Metro northwards into Seattle. This gave people time to migrate to the more desirable location (from Vancouver to Seattle). By turn 72, drawn by Seattle's superior connectivity in the rail network, over 300,000 people had migrated from Vancouver. This made land acquisition in Vancouver much cheaper.
By turn 73, I had four cities over population one million (black border):
On turns 79-81 I used the trade winds to rapidly explore the sea in the far south and south-east.
By turn 102, I had 9 big million-plus cities:
Land value in these cities was bolstered by two metro lines. A second line was required in the north-western forest due to geometric constraints (branching is not allowed):
On turn 168, I stopped building, and just started saving money to get the 6th and final tech.
Game finished on turn 173. At this time, I had 6 cities over 2.5 million:
Thursday, March 2, 2017
Kansai Rail Simulator - LP
"Kansai Rail Simulator" is coming.
Play as GERMANY:
Play as KOREA:
On January 25, we began work on a powerful rail-network simulation game. It has now reached an advanced stage, and is undergoing testing.
I am inviting current beta testers to post their Let's Plays in the comments section below. Please take a look at these exciting game records!
Play as GERMANY:
Play as KOREA:
On January 25, we began work on a powerful rail-network simulation game. It has now reached an advanced stage, and is undergoing testing.
I am inviting current beta testers to post their Let's Plays in the comments section below. Please take a look at these exciting game records!
Copyright 2017 Matthew J Curran.
Friday, December 23, 2016
Encyclopedia of Drunken Walks
"God does not play dice" vs "God does not waste computational resources"
Drunken walks are ideal for map generation for 3 reasons:
- The generated map is inherently fractal.
- The generated map is definitively random.
- The map can be generated dynamically (on the fly). This dynamic map generation allows for unlimited map size (boundless and infinite).
Drunken walks can be biased to favor any combination of the 6 cardinal/absolute directions (NW, NE, East, SE, SW, West) and the 6 relative directions (straight forward = 12:00, right forward = 2:00, right backward = 4:00, straight backward = 6:00, left backward = 8:00, left forward = 10:00).
These biases can be encoded in 6 weights for cardinal/absolute directions, and 6 weights for relative directions (relative to the current direction of movement).
A drunken walk pattern can thus be defined by 12 weights, and we call this collection of weights the "Direction Tensor". The word "tensor" is used here to mean roughly "an object whose shadow is a vector". At any given point in time, the likelihood of moving in each direction is proportional to the product of the cardinal/absolute weight, and the corresponding relative weight (each relative direction corresponds to an absolute direction, with respect to the current direction of movement).
The effects of chaging the 6 cardinal/absolute weights are fairly predictable, so this study examines only the effects of relative weightings (the 6 cardinal/absolute weights are taken to be equal to each other, so there are no cardinal biases).
- Example Patterns -
Limiting movement to backwards right and left (4:00 and 8:00) leads to a relatively compact but elongated form:
 |
| 50% right backwards (4:00), 50% left backwards (8:00). |
 |
| 66% right backwards (4:00), 33% left backwards (8:00). |
 |
| 66% straight forward (12:00), 33% right forward (2:00). |
 |
| 50% right forward (2:00), 50% left forward (10:00). [example 1/2] |
 |
| 50% right forward (2:00), 50% left forward (10:00). [example 2/2] |
 |
| 20% straight forward (12:00), 20% right forward (2:00), 20% right backward (4:00), 20% left backward (8:00), 20% left forward (10:00). [example 1/3] |
 |
| 20% straight forward (12:00), 20% right forward (2:00), 20% right backward (4:00), 20% left backward (8:00), 20% left forward (10:00). [example 2/3] |
 |
| 20% straight forward (12:00), 20% right forward (2:00), 20% right backward (4:00), 20% left backward (8:00), 20% left forward (10:00). [example 3/3] |
- VBA Code (Class Module) -
'6 weights for the 6 absolute directions:
Public NW As Single
Public NE As Single
Public East As Single
Public SE As Single
Public SW As Single
Public West As Single
'6 weights for the 6 relative directions:
Public StraightForward As Single
Public RightForward As Single
Public RightBackward As Single
Public StraightBackward As Single
Public LeftBackward As Single
Public LeftForward As Single
'6 numbers for current fractional likelihood of each absolute direction:
Public ProbabilityNW As Single
Public ProbabilityNE As Single
Public ProbabilityEast As Single
Public ProbabilitySE As Single
Public ProbabilitySW As Single
Public ProbabilityWest As Single
Public Function GetDirection(ByVal Previous As Location, ByVal Current As Location)
Dim Direction As String
Dim SouthShift, EastShift As Integer
SouthShift = Current.Row - Previous.Row
EastShift = Current.Col - Previous.Col
Direction = "resting"
If SouthShift = 0 And EastShift = 1 Then Direction = "East"
If SouthShift = 0 And EastShift = -1 Then Direction = "West"
If SouthShift = 1 And EastShift = 0 Then Direction = "SE"
If SouthShift = 1 And EastShift = -1 Then Direction = "SW"
If SouthShift = -1 And EastShift = 1 Then Direction = "NE"
If SouthShift = -1 And EastShift = 0 Then Direction = "NW"
GetDirection = Direction
End Function
Public Sub CalculateProbabilities(ByVal Direction As String)
'The public variable "Direction" should be set before calling this sub.
Dim AbsoluteWeights(6) As Single
Dim RelativeWeights(6) As Single
Dim CombinedWeights(6) As Single
Dim Counter, RotatingCounter As Integer
Dim TotalWeights As Single
AbsoluteWeights(0) = Me.NW
AbsoluteWeights(1) = Me.NE
AbsoluteWeights(2) = Me.East
AbsoluteWeights(3) = Me.SE
AbsoluteWeights(4) = Me.SW
AbsoluteWeights(5) = Me.West
RelativeWeights(0) = Me.StraightForward
RelativeWeights(1) = Me.RightForward
RelativeWeights(2) = Me.RightBackward
RelativeWeights(3) = Me.StraightBackward
RelativeWeights(4) = Me.LeftBackward
RelativeWeights(5) = Me.LeftForward
TotalWeights = 0
'Rotate RelativeWeights depending on Direction:
Select Case Direction
Case "NW"
For Counter = 0 To 5
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(Counter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "NE"
For Counter = 0 To 5
RotatingCounter = (Counter - 1) Mod 6
'We need the next line, because vba does "mod" wrong.
If RotatingCounter < 0 Then RotatingCounter = RotatingCounter + 6
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(RotatingCounter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "East"
For Counter = 0 To 5
RotatingCounter = (Counter - 2) Mod 6
If RotatingCounter < 0 Then RotatingCounter = RotatingCounter + 6
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(RotatingCounter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "SE"
For Counter = 0 To 5
RotatingCounter = (Counter - 3) Mod 6
If RotatingCounter < 0 Then RotatingCounter = RotatingCounter + 6
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(RotatingCounter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "SW"
For Counter = 0 To 5
RotatingCounter = (Counter - 4) Mod 6
If RotatingCounter < 0 Then RotatingCounter = RotatingCounter + 6
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(RotatingCounter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "West"
For Counter = 0 To 5
RotatingCounter = (Counter - 5) Mod 6
If RotatingCounter < 0 Then RotatingCounter = RotatingCounter + 6
CombinedWeights(Counter) = AbsoluteWeights(Counter) * RelativeWeights(RotatingCounter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
Case "resting"
'If the animal rested on the last turn, absolute/cardinal movement bias controls:
For Counter = 0 To 5
CombinedWeights(Counter) = AbsoluteWeights(Counter)
TotalWeights = TotalWeights + CombinedWeights(Counter)
Next Counter
End Select
'Normalize the probabilities so they add up to 1:
If TotalWeights <> 0 Then
For Counter = 0 To 5
CombinedWeights(Counter) = CombinedWeights(Counter) / TotalWeights
Next Counter
End If
Me.ProbabilityNW = CombinedWeights(0)
Me.ProbabilityNE = CombinedWeights(1)
Me.ProbabilityEast = CombinedWeights(2)
Me.ProbabilitySE = CombinedWeights(3)
Me.ProbabilitySW = CombinedWeights(4)
Me.ProbabilityWest = CombinedWeights(5)
End Sub
Public Sub NormalizeProbabilities(ByVal TotalWeights As Single)
'Use zero to indicate "recalculate TotalWeights":
If TotalWeights = 0 Then
TotalWeights = Me.ProbabilityNW + Me.ProbabilityNE + Me.ProbabilityEast _
+ Me.ProbabilitySE + Me.ProbabilitySW + Me.ProbabilityWest
End If
'If it actually is zero (based on math), then use "absolute values":
If TotalWeights = 0 Then
Me.CalculateProbabilities ("resting")
Else
Me.ProbabilityNW = Me.ProbabilityNW / TotalWeights
Me.ProbabilityNE = Me.ProbabilityNE / TotalWeights
Me.ProbabilityEast = Me.ProbabilityEast / TotalWeights
Me.ProbabilitySE = Me.ProbabilitySE / TotalWeights
Me.ProbabilitySW = Me.ProbabilitySW / TotalWeights
Me.ProbabilityWest = Me.ProbabilityWest / TotalWeights
End If
End Sub
Copyright 2016 Matthew J Curran.
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this code except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
Monday, November 28, 2016
Exodus To Kobe 2.0
This version allows domestication of animal herds.
 |
| Click "Update Radar" any time you move over or next to a new herd. |
 |
| Click "Show All my Herds" to view all the animals you have domesticated. |
 |
| Click "Show my Fastest Herds" to view your movement cost over different terrain. |
 |
| You can play as either Germany, Russia, or Korea (single or multi-player). Your goal is still to find Kobe. |
You must enable macros for this game to run in Excel. Never run Excel macros from questionable or unverified websites.
Copyright 2016 Matthew J Curran. Full license details in Module 1 of the VBA code.
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
Sunday, November 20, 2016
Co-Ex World Explorer - Third Release: Exodus To Kobe
In this mini-game, you can play as either Germany or Korea (single or multi-player). Your goal is to find Kobe.
Most of the key game features (e.g. domestication and evolution of animals) still remain to be implemented. This fully functional mini-game serves primarily to illustrate the power of Dynamic Map Generation (行動的地図開発).
Here are five unique starting maps, all dynamically generated from the same seed map (with the location of Japan semi-randomized):
For single player mode, simply delete the contents of row 7, col 1 in "Maps" tab.
To add a third player, type "Germany", "Korea", or "random" in row 8, col 1 of "Maps" tab, and also make sure to create three additional tabs, which you must "move to end". Type a color index in row 8, col 2. Of course, due to the semi-randomized location of Japan, the third player will be at a disadvantage.
You must enable macros for this game to run in Excel. Never run Excel macros from questionable or unverified websites.
Most of the key game features (e.g. domestication and evolution of animals) still remain to be implemented. This fully functional mini-game serves primarily to illustrate the power of Dynamic Map Generation (行動的地図開発).
Here are five unique starting maps, all dynamically generated from the same seed map (with the location of Japan semi-randomized):
 |
| Germany in NW, Korea in NE, Japan to the south. |
 |
| In this map, the Korean peninsula may turn out to be an island. |
 |
| In this map, a Denmark-like formation separates the North Sea and the Baltic. |
 |
| In this map, Germany and Japan have grown together to form a single continent. |
 |
| The Osaka plain is clearly visible to the east of Kobe (forested tile). |
For single player mode, simply delete the contents of row 7, col 1 in "Maps" tab.
To add a third player, type "Germany", "Korea", or "random" in row 8, col 1 of "Maps" tab, and also make sure to create three additional tabs, which you must "move to end". Type a color index in row 8, col 2. Of course, due to the semi-randomized location of Japan, the third player will be at a disadvantage.
You must enable macros for this game to run in Excel. Never run Excel macros from questionable or unverified websites.
Copyright 2016. Full license details in Module 1 of the VBA code.
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
Subscribe to:
Posts (Atom)